using newtype and coerce

郗昀彥

Thursday

Who?

郗(ㄔ)昀彥

jaiyalas
https://www.github.com/jaiyalas

functional programming language
type theory and system
program derivation and construction

Prelude

Irrefutable

Patterns that never fail to match
are said to be irrefutable.

base case

wild pattern
- ```
case v of _ -> comp
```
single variable
- ```
case v of a -> comp
```

lazy pattern

case v of ~pat -> comp

case [] of {(x:xs) -> 42}

Error: Non-exhaustive patterns in case

case [] of {~(x:xs) -> 42}

Value: 42

case [] of {~(x:xs) -> x}

Error: Irrefutable pattern failed for pattern (x : xs)

as pattern

case v of a@pat -> comp

Pattern a@pat is irrefutable if pat is.

case [] of {a@ (x:xs) -> a}

Error: Non-exhaustive patterns in case

case [] of {a@ ~(x:xs) -> a}

Value: []

case [] of {a@ ~(x:xs) -> x}

Error: Irrefutable pattern failed for pattern (x : xs)

The `newtype`

data

Algebraic Datatype Declarations

data D a b = C1 a b
           | C2 b b
           | C3

newtype

Datatype Renamings

newtype N0 = Cn0 Bool
newtype N1 a = Cn1 [Int]

1 constructor, 1 parameter (field)
wrapper

comparison

Given a data structure

data D = C0 | C1 | C2 | C3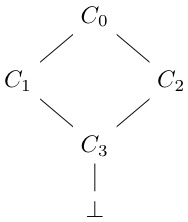

using data..

data W = Cd D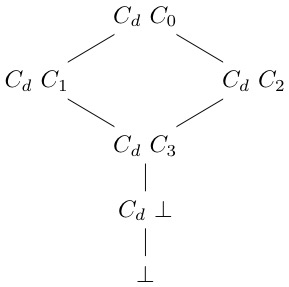

using newtype..

newtype N = Cn D

newtype constructor is unlifted

experiment

```
case (Cd ⊥) of (Cd a) -> 42
=> 42
```
```
case ⊥ of (Cd a) -> 42
=> ⊥
```
```
case (Cn ⊥) of (Cn a) -> 42
=> 42
```
```
case ⊥ of (Cn a) -> 42
=> 42
```

wait a sec, how is the last one not a ⊥?

Irrefutable pattern

The last way to construct one

case v of N pat -> comp

Pattern N pat is irrefutable if pat is.

how?

case ⊥ of (N pat) -> e
    => case ⊥ of pat -> e

case (N v) of (N pat) -> e
    => case v of pat -> e

introduces a new type whose representation
is the same as an existing type
- may require no run-time overhead
must be explicitly coerced from or to the original type
- constructor
- constructor in pattern / record
the new type is called wrapper
- no default instances

Example

Monoid

class Monoid a where
        mempty  :: a
        mappend :: a -> a -> a

Bool as a Monoid

Which definition of mappend we want?
and, or, xor, .. ?

newtype All = All { getAll :: Bool }

instance Monoid All where
    mempty = All True
    All x `mappend` All y = All (x && y)

newtype Any = Any { getAny :: Bool }

instance Monoid Any where
    mempty = Any False
    Any x `mappend` Any y = Any (x || y)

The Shortcomings

Given

newtype HTML = MkHTML String

may require no run-time overhead
- trans :: [HTML] -> [String]
no any instances
- some can be generated by deriving
- some cannot: e.g. Functor

may require no run-time overhead

Slow!

trans :: [HTML] -> [String]
trans [] = []
trans (MkHTML s:xs) = x:(trans xs)

Coerce!

Unsafe.Corece
- ```
unsafeCoerce :: a -> b 
```
Data.Corece
- ```
coerce :: Coercible * a b =>
a -> b 
```

Fast!

trans' :: [HTML] -> [String]
trans' = unsafeCoerce

trans'' :: [HTML] -> [String]
trans'' = coerce

Given

data D = C ...
newtype N = MkN D

and F is a type-level function,

Haskell(GHC) do knows
- N = D
Haskell(GHC) don't knows
- F N = F D

unsafeCoerce: force F N = F D
coerce: Coercible (F N) (F D) then F N = F D

how do we (or GHC) know (F N) and (F D)
are coercible?

No default instances

Sure we can

deriving ( Eq
         , Ord
         , Read
         , Show
         , Bounded
         , Generic)

Is this ok?

deriving Functor

-XGeneralizedNewtypeDeriving
- inherit instances

newtype Age = MkAge Int deriving Num

newtype Ls a = L [a] deriving Functor

-XGeneralizedNewtypeDeriving

inherit instances

coerce :: Coercible * a b =>
a -> b